Coloring Maps Graph Theory - Coloring Pages For Kids
21 110 Conflict Graphs
Four Color Theorem Simple English Wikipedia The Free Encyclopedia
It is mathematics which studies phenomena which are not continuous but happens in small or discrete chunks.
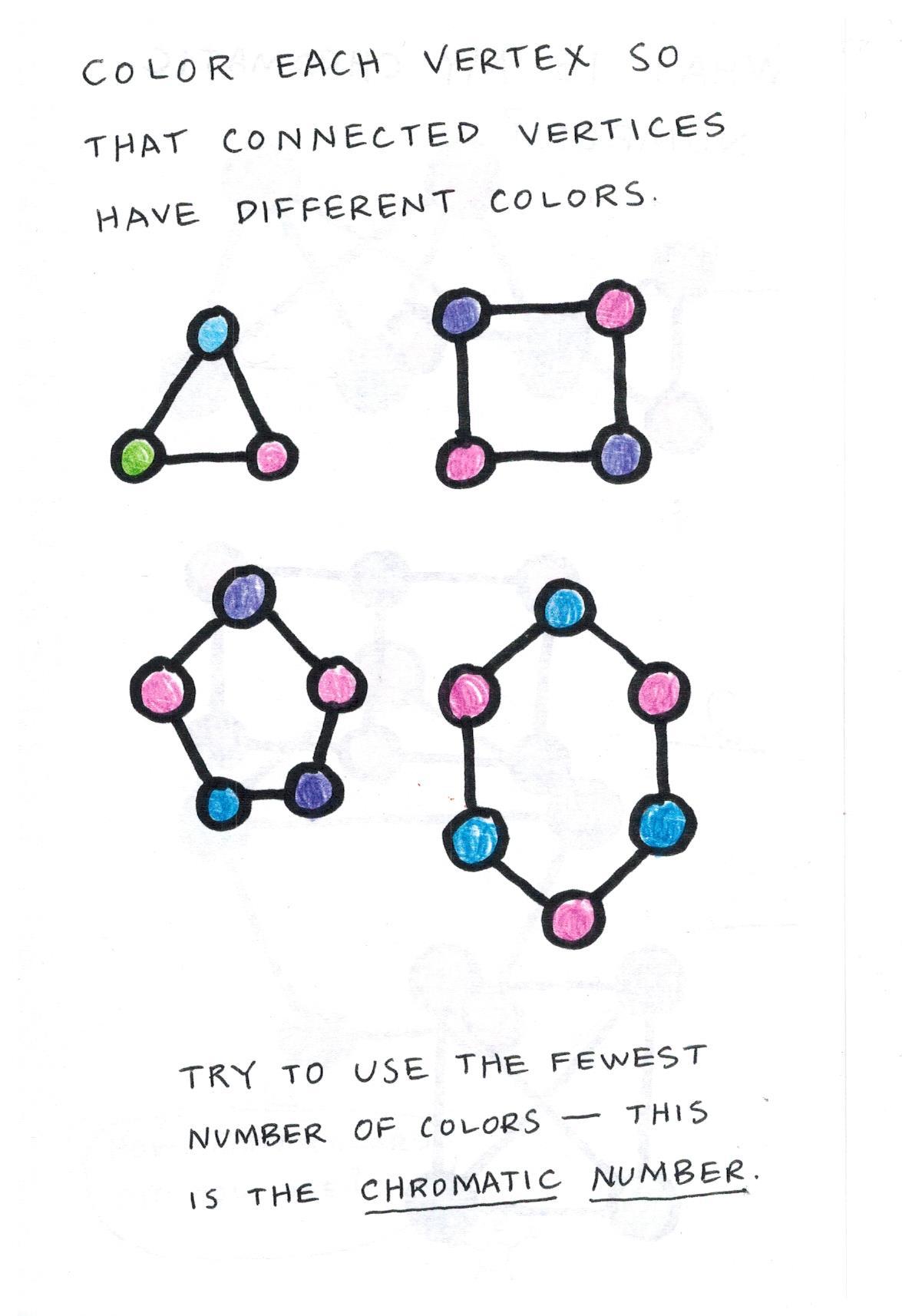
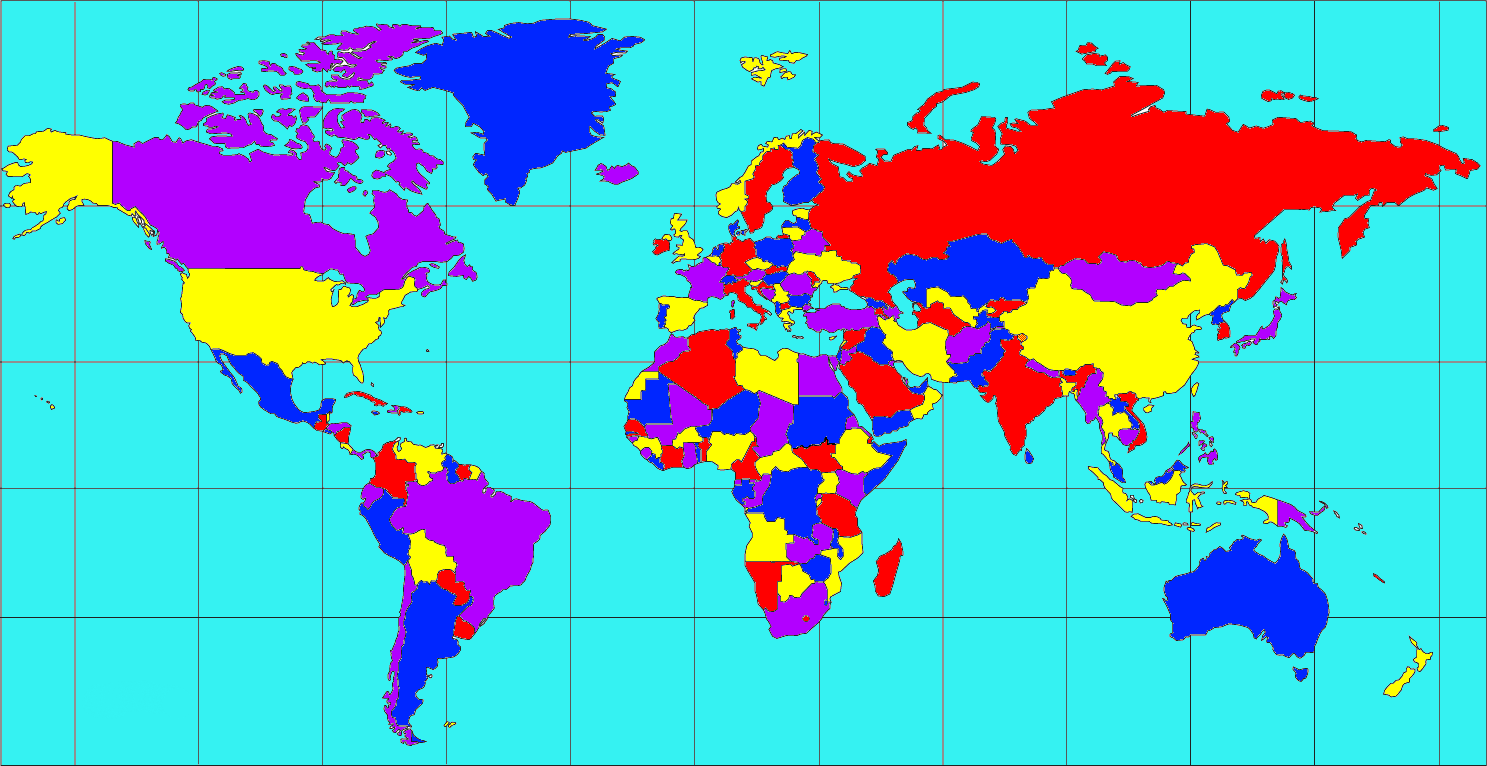
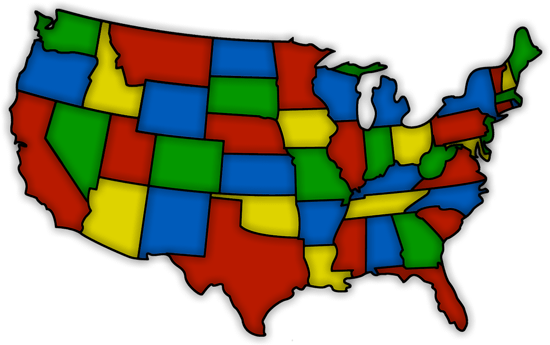
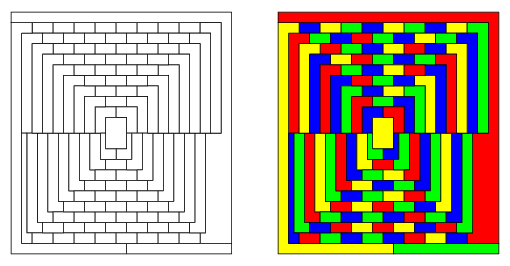
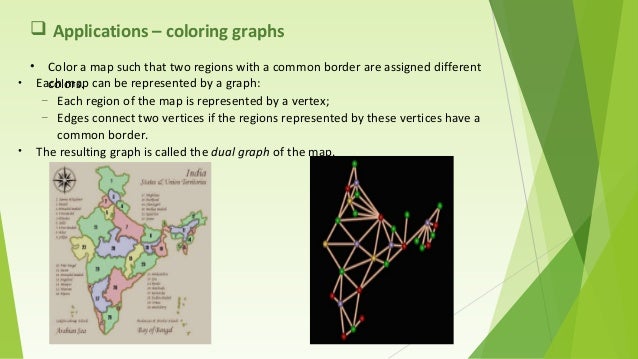
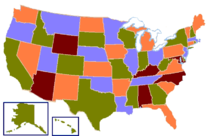
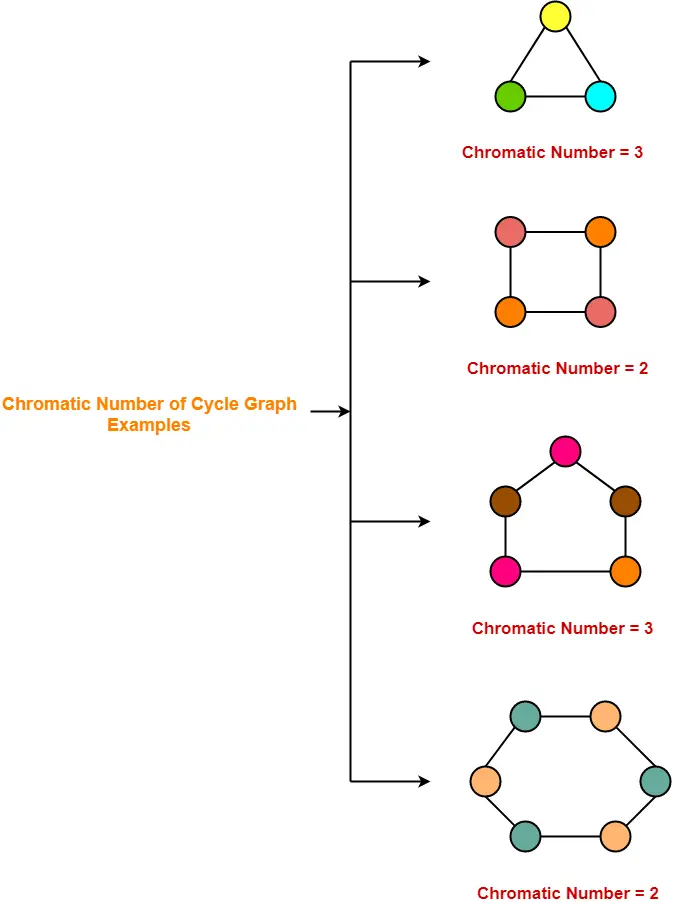
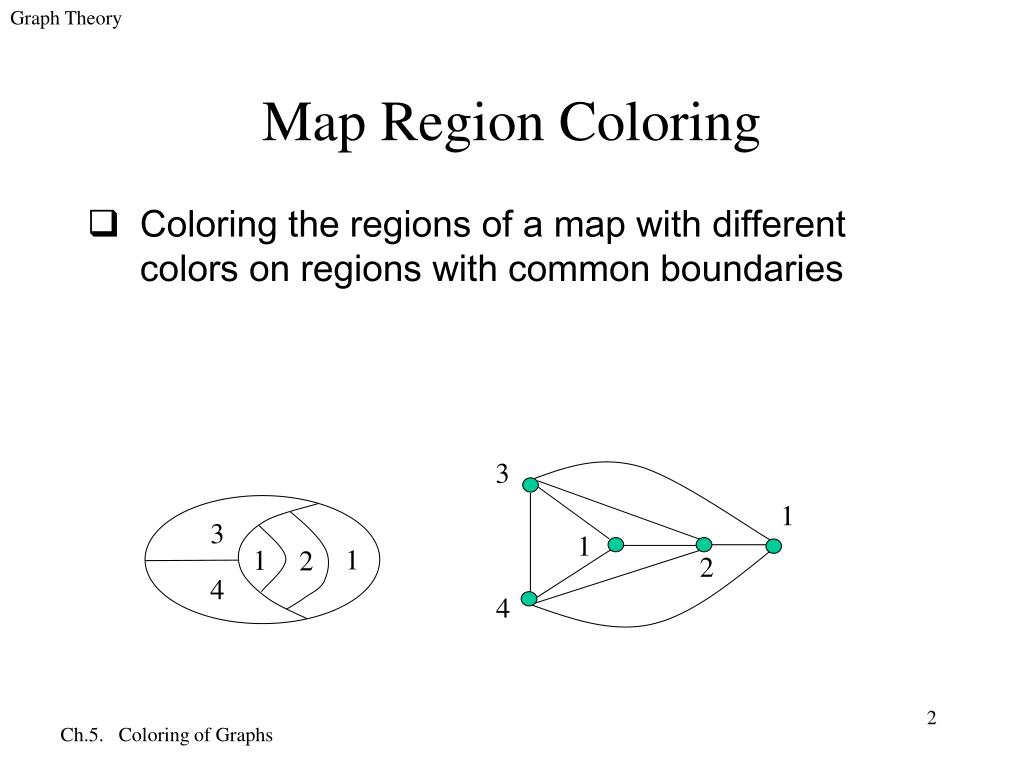
Coloring maps graph theory. It is impossible to color the graph with 2 colors so the graph has chromatic number 3. We might also want to use as few different colours as. The chromatic number x g chig x g of a graph g g g is the minimal number of colors for which such an. Graph theory gives us both an easy way to pictorially represent many major mathematical results and insights into the deep theories behind them.
Courses are represented by vertices. Applications of graph coloring graph theory and its applications coloring of a graph is an assignment of colors either to the edges of the graph g or to vertices or to maps in such a way. In this course among other intriguing applications we will see how gps systems find shortest routes how engineers design integrated circuits how biologists assemble genomes why a political map. A graph coloring is an assignment of labels called colors to the vertices of a graph such that no two adjacent vertices share the same color.
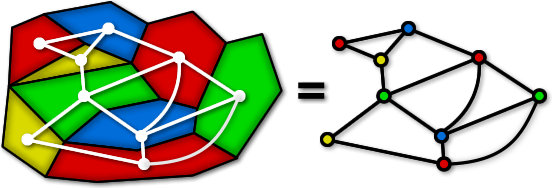
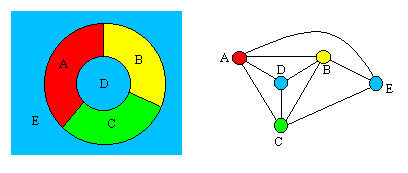
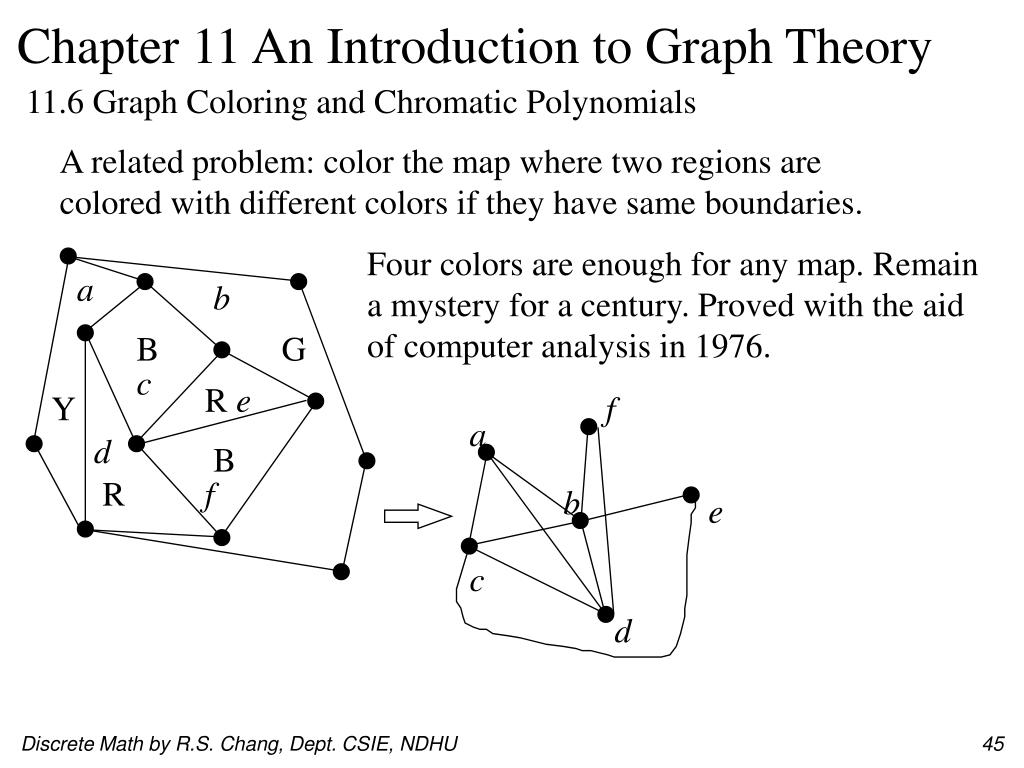
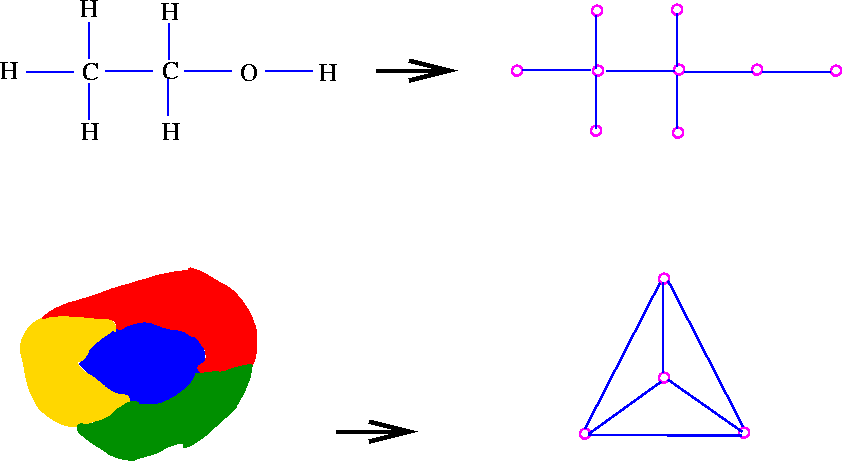
In graph theory graph coloring is a special case of graph labeling. Coloring regions on the map corresponds to coloring the vertices of the graph. Search and read the full text of patents from around the world with google patents and find prior art in our index of non patent literature. Graph coloring and scheduling convert problem into a graph coloring problem.
Two vertices are connected with an edge if the corresponding courses have a student in common. This number is called the chromatic number and. In graph theoretic terms the theorem states that for loopless planar graph the chromatic number of its dual graph is. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
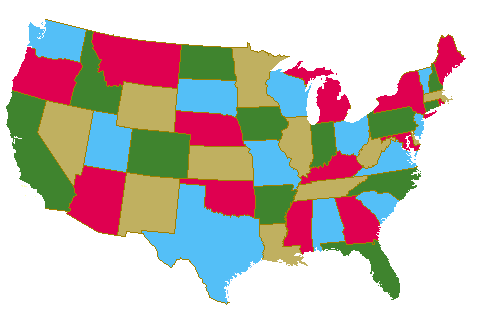
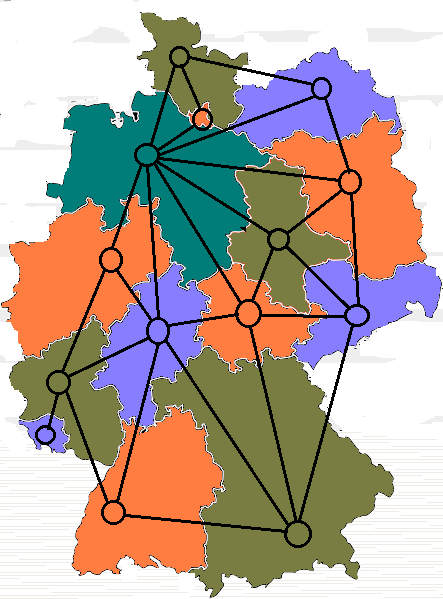
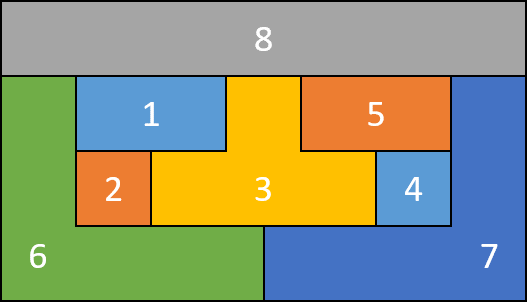
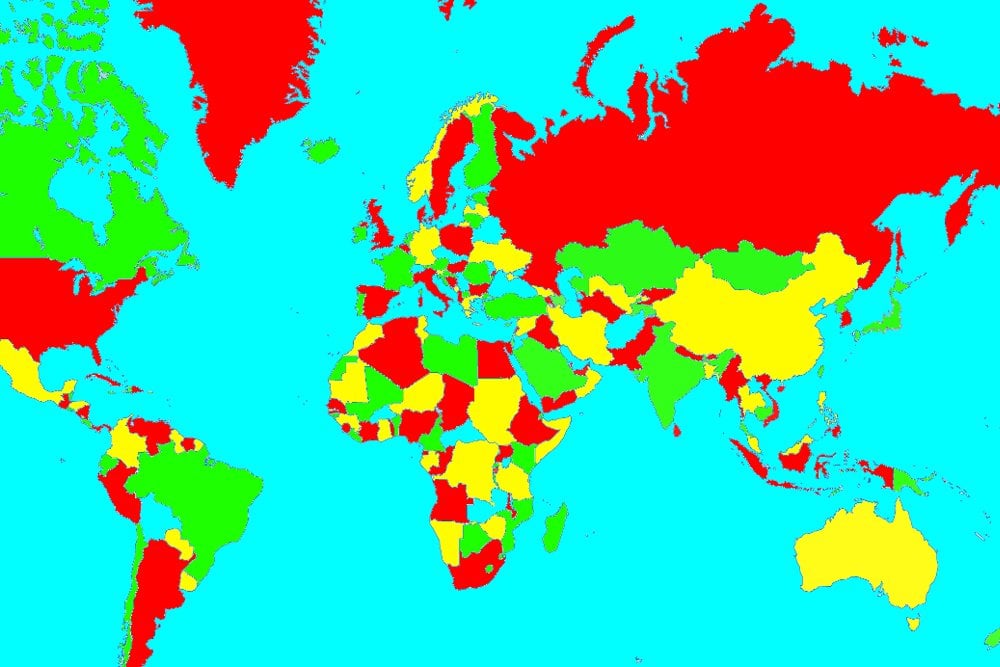
This is called a vertex coloringsimilarly an edge coloring assigns a color to each. The intuitive statement of the four color theorem given any separation of a plane into contiguous regions the regions can be colored using at most four colors so that no two adjacent regions have the same color needs. In general given any graph gtext a coloring of the vertices is called not surprisingly a vertex coloring. As we zoom out individual roads and bridges disappear and instead we see the outline of entire countries.
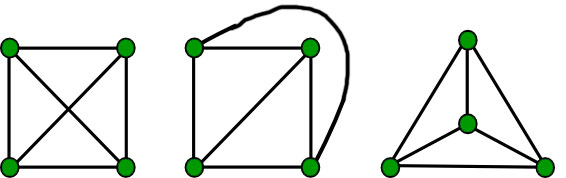
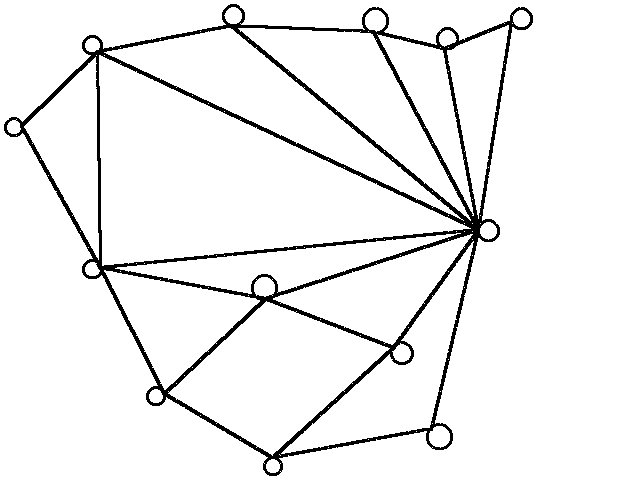
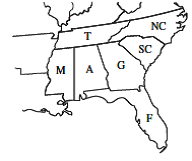
When colouring a map or any other drawing consisting of distinct regions adjacent countries cannot have the same colour. Map coloring to graph coloring part of a unit on discrete mathematics. Precise formulation of the theorem. A graph coloring for a graph with 6 vertices.
Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints. It is the mathematics of computers. 1007 3137 3157 3203 4115 3261 4156 4118. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color.
Some areas include graph theory networks counting techniques coloring theory game theory and more.
Overview Of Graph Colouring Algorithms
Graph Coloring Wikipedia
Applications Of Graph Theory Dharwadker Ashay Pirzada Shariefuddin 9781466397095 Amazon Com Books
Map Colouring Graphs And Networks Mathigon
Four Color Theorem Wikipedia
Maps Mania Fun With Graph Theory Maps
Graph Theory
Graph Coloring Set 1 Introduction And Applications Geeksforgeeks
Seminar Assignments The Four Color Theorem Math 410 Studocu
Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins
Graph Coloring Vertex Graph Theory Four Color Theorem Png 1275x1088px Graph Coloring Bipartite Graph Body Jewelry
Euler S Map Theorem A Surprising Activity Occupy Math
Map Coloring And Some Of Its Applications
Map Coloring And Some Of Its Applications
Graph Theory Xmind Mind Mapping Software
Math Explorers Club
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins
Map Coloring And Some Of Its Applications
A Solution To The Map Coloring Problem Of The World With Four Download Scientific Diagram
Http Cgm Cs Mcgill Ca Godfried Teaching Dm Reading Assignments Map Graph Coloring Pdf
5 4 Coloring Mathematics Libretexts
Ppt Graph Theory And Graph Coloring Lindsay Mullen Powerpoint Presentation Id 2065357
Coloring The Plane The Intrepid Mathematician
Applications Of Graph Theory Main
The Four Color Theorem 1 The Map
Map Coloring And Mathematical Games
Four Color Map Problem An Introduction To Graph Theory Teaching Resources
Graph Theory
Graph Theory
5 4 Coloring Mathematics Libretexts
4 Four Color Theorem Png Cliparts For Free Download Uihere
Torus Coloring From Wolfram Mathworld
Mmw Exercise Set 6 4 Vertex Graph Theory Graph Theory Free 30 Day Trial Scribd
Graph Colouring Tress In Graph Theory Chromatic Powerpoint Presentation Free Online Download Ppt Bf1v2y
Graph Theory
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcset8ejpyxqu7ymqm4yvsb4s5s1kmgzjwjb 0a9 S45uuwys8mh Usqp Cau
Https Arxiv Org Pdf 1708 07442
Is There A Proof That A Map Of The United States Requires 4 Colors Puzzling Stack Exchange
Application Of Graph Coloring In Map Coloring And Gsm Mobile Phone Networks Graph Theory Vertex Graph Theory
The Four Color Theorem
Graph Coloring And Its Applications
Math For Liberal Studies The Greedy Coloring Algorithm Youtube
Mcgregor Map From Wolfram Mathworld
Decades Old Graph Problem Yields To Amateur Mathematician Quanta Magazine
Four Color Theorem Disproof Mathematics Stack Exchange
Graph Coloring Using Cuda I Team Members
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsatqw53cvycv 5 Jjfeupu6efa8ks 0r9dylx P5vquq8lgmq1 Usqp Cau
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcsyxebr6hc9hhasir92jsmkdb Snxju6ux176foujfmxecnspmq Usqp Cau
Graph Colouring Computer Science Unplugged
The Four Color Problem With High Probability
Map Cartoon Png Download 640 640 Free Transparent Graph Coloring Png Download Cleanpng Kisspng
The Four Color Theorem
Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins
How To Find All Proper Colorings Four Coloring Of A Graph With A Brute Force Algorithm Mathematics Stack Exchange
Mathematician Disproves Hedetniemi S Graph Theory Conjecture Quanta Magazine
Graph Coloring And Its Applications
Graph Coloring Or Proof By Crayon Math Programming
Graph Coloring Github Topics Github
Graph Theory Brilliant Math Science Wiki
Aprildt
Graph Theory Coloring Maps By Rachael Schauer
Four Color Theorem Wikipedia
Ppt An Introduction To Graph Theory Powerpoint Presentation Free Download Id 1273252
Graph Coloring In Graph Theory Chromatic Number Of Graphs Gate Vidyalay
Map Coloring And Conflict Resolution Occupy Math
Coloring Graphs This Handout Coloring Maps And Graphs Ppt Video Online Download
Adversarial Map Coloring Book Proofs
Ppt Chapter 5 Powerpoint Presentation Free Download Id 672733
The Four Color Theorem
Mathematician Disproves Hedetniemi S Graph Theory Conjecture Quanta Magazine
The Four Color Theorem Its Surreal Simplicity Critical By Jesus Najera Cantor S Paradise Medium
Four Color Theorem Wikipedia
Math For Seven Year Olds Graph Coloring Chromatic Numbers And Eulerian Paths And Circuits Joel David Hamkins
Graph Algorithms
Coloring The Four Color Theorem
Graph Theory
Pdf A Performance Comparison Of Graph Coloring Algorithms
Solved Coloring Graphs And Maps Hundreds Of Years Ago Map Chegg Com
Four Color Theorem What Is Four Color Map Theorem
Graph Coloring Graph Theory Planar Graph Four Color Theorem Mathematics Transparent Background Png Clipart Pngguru
Ams Feature Column From The Ams
A Sql Approach To Graph Coloring Applied To Maps Carto Blog
Map Colouring Problem Mathematics Britannica
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcq Hrrlace Ff5lqm4ngqvhmeyzxyc9uoompywvoma Usqp Cau
Http Web Math Princeton Edu Math Alive 5 Notes2 Pdf
Applications Of Graph Colouring Youtube
Graph Theory
Four Color Theorem Brilliant Math Science Wiki
Graph Coloring Or Proof By Crayon Math Programming
Introduction To Graph Colouring Youtube
The Four Color Map Theorem Numberphile Youtube
Coloring The Four Color Theorem
1 5 Graph Theory Graph Theory The Branch Of Mathematics In Which Graphs And Networks Are Used To Solve Problems Ppt Download
Http Web Math Princeton Edu Math Alive 5 Notes2 Pdf
Coloring The Four Color Theorem
Coloring Graphs Part 2 Coloring Maps The Four Color Problem Youtube
Adversarial Map Coloring Book Proofs
Aim What Does Map Coloring Have To Do With Graph Theory Ppt Download
Graph Coloring Or Proof By Crayon Math Programming
Greedy Coloring Wikipedia
Graph Theory Rld World
